Р. А. Симонов. "Мисячные числа"
Из приведенной выдержки следует, что «мисячные числа» это календарные элементы, известные в науке под названием «солнечных регуляров».
И. А. Климишин воспроизводит в своей книге точно такой ряд значений для тех же месяцев, указывая, что это «солнечные регуляры в таком порядке:

Климишин И. А. Календарь и хронология. 2-е изд. М., 1985. С. 278. Ссылки в дальнейшем изложении даются на это издание).
В древнерусском тексте говорится, что к числу «настоящего года Богословли руки» прибавляется «мисячное число». Числа «Богословли руки», или по-научному конкурренты: 1, 2, 3, 5, 6, 7, 1, 3, 4, 5, 6, 1, 2, 3, 4, 6, 7, 1, 2, 4, 5, 6, 7, 2, 3, 4, 5, 7 связаны с календарным циклом в 28 лет, получившим название «солнечного круга». Порядок конкуррент взят в той последовательности, которая указывается для них в цитированной рукописи № 632, л. 72. Год, записанный в эре от «сотворения мира», делили на 28, остаток назывался солнечным кругом текущего года. О том, что такое солнечный круг и как его находить, было известно в древнерусский период. Например, об этом идет речь в календарном трактате 1136 г. «Учение им же ведати человеку числа всех лет» Кирика Новгородца.
Как сообщает И. А. Климишин, «...конкурренты, или солнечные эпакты ...широко использовались начиная с VIII в. для отождествления календарной даты с днем недели. Первым, но отнюдь е главным назначением конкурренты было указать день недели, на который в том или другом году приходилось 24 марта: при конкурренте 1 это воскресенье, 2 - понедельник, 3 - вторник, 4 - среда, 5 - четверг, 6 - пятница, 7 - суббота» (с. 94).
Так, для определения дня недели 24 марта 1136 г, надо перевести дату в эру от сотворения мира: 6644 г. (=1136+5508) и разделить ее па 28. В остатке получится восемь, т. о. в 1136 г. шел 8-й солнечный круг. Кириком Новгородцем соответствующие расчеты были сделаны. В ряду конкурреит восьмым знаком оказывается 3, что отвечает вторнику. Как правильно вычислил Кирик, пасха в 1136 г. была 22 марта, а так как христианская пасха бывает в воскресенье, что 24 марта приходилось на вторник. Следовательно, результат соответствует действительности.
Существует календарный элемент, называемый в современной науке «месячным коэффициентом», представляющий собой сумму конкурренты и регуляра, из которой вычитается единица: К (месячный коэффициент) = конкуррента + регуляр - 1. Если величина месячного коэффициента окажется больше семи, то нужно вычесть семерку: К = конкуррента + регуляра - 1 - 7 = конкуррента + регуляра - 8. Последняя формула соответствует правилу, которое изложено в древнерусском тексте. Следовательно, календарный смысл текста мог заключаться в определении месячного коэффициента.
Для чего нужно знать месячный коэффициент? Как разъясняет И. А. Климишин, месячный коэффициент является важным элементом вечного юлианского календаря, математическую модель которого можно представить в виде зависимости:
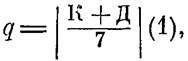
где К - месячный коэффициент, Д - число месяца. Вертикальные черточки по краям дроби означают, что берется остаток от деления на семь. В остатке будет какое-то из чисел: 1, 2, 3, 4, 5, 6, 7 (или 0). По ним определяется день недели в соответствии с приведенным выше правилом: 1 - воскресенье, 2 - понедельник и т. д. (с. 99).
Применим указанную формулу для проверки того, что днем недели 22 марта 1136 г. было воскресенье (пасха). Конкуррента 1136 г.= 3, регуляра марта = 5. Находим месячный коэффициент К = конкуррента + регуляра - 8 (что соответствует правилу публикуемого текста): К = 3 + 5 - 8 = 0. Для К = 0 и Д = 22 выражение (1) даст
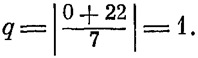
Остаток q=l соответствует воскресенью. Следовательно, проверка дает положительный результат.
Публикуемый текст находится в рукописи, на которую автору настоящей статьи любезно было указано А. А. Туриловым и А. В. Чернецовым. Начинается она словами «Предисловие святцам. Творение грешного раба Ивана Рыкова...» Книга является сводом данных о календарных понятиях, включая единицы счета времени, а также сведений по астрономии, астрологии и пр. Начальная часть рукописи, по-видимому, является «творением» Ивана Рыкова. Следующий за ней материал, включая публикуемый текст, не может быть безусловно приписан Ивану Рыкову, но его авторство исключать нельзя. В таком случае публикуемый текст отражает календарные традиции, существовавшие во Пскове во второй половине XVI в., когда здесь жил указанный древнерусский писатель и ученый.
Календарный текст в рукопись второй половины XVII в., где он встречается, возможно, попал из компиляции Ивана Рыкова XVI в. Поэтому важное значение для решения вопроса о первоначальном облике календарного текста имеет разыскание его других списков. Однако независимо от решения вопроса о списках, опубликованный текст имеет самостоятельное научное значение, связанное с применением солнечных регуляров («мисячных чисел») как календарных элементов.
Как далеко в древность уходит использование па Руси «мисячных чисел» (регуляров)? Возможно их имеет в виду Кирик, когда говорит о календарном назначении понятия «солнечного круга»: «При помощи его и вычисляй пасху и все месяцы». Как конкретно нужно вычислять, Кирик не объясняет. Публикуемый в настоящей статье текст позволяет высказать следующую гипотезу по этому вопросу. Сопоставляя начальные слова опубликованного текста: «А Богословлею рукою искати наус (?) настатя книжных месяцей и лунных праздников...» с выдержкой из Кирика, можно усмотреть определенную аналогию. Пасха - центральный лунный праздник христианского календаря. В обоих текстах, скорее всего, идет речь об одном и том же: о вычислении пасхи и других с этим днем связанных лунных праздников.
Подведя итог, можно сказать, что публикуемый текст способствует прояснению истории древнерусских календарных традиций в области разработки вычислений в системе «вечного календаря». Однако остается неизвестным, к какому этапу исторического развития древнерусской календарной традиции относится текст. Неясно, насколько далеко в глубь веков можно отодвигать древнерусское называние солнечных регуляров «мисячными числами». Настоящую публикацию нужно рассматривать как одну из попыток изучения древнерусского календарного источника, дальнейшее обнаружение и исследование подобных которому будет способствовать решению историко-научного вопроса об употреблении на Руси расчётных календарных приемов (вероятно связанных с функционированием «вечного календаря») на основе использования солнечных регуляров («мисячных чисел»).
<< Назад Вперёд>>









